ＳＳＨアラカルト

Home>
明和SSH>
ＳＳＨアラカルト2018

ＳＳＨアラカルト

◇令和元年度　ＳＳＨ夏の事業

昨年度から「SSH 夏の事業」の改善を進めており、本年度は、２年生で開講している「課題探究」へと結びつけるために、「課題探究基礎講座」を「課題探究入門講座」と「課題探究自主講座」に分け、「課題探究自主講座」では、「課題探究」で行われる研究に対する基礎実験や今後の実験の進め方などのアドバイスを行いました。また、昨年度「SSHサイエンスツアー」から独立させた「一日研究員体験」をより充実したものにし、さらに、「さくらサイエンス交流会」に代わり、本校が主体となって東海地区に留学している外国人高校生・大学生に課題研究を英語で発表する「明和グローバルサイエンス交流会」を実施しました。こうした「SSH夏の事業」を盛り上げるために、大型ポスターを作製した結果、どの講座も盛況で、生徒は、日頃の授業では味わうことができない様々な科学の諸分野の活動に直接触れたり、参加したりすることで『探究心』を高揚させることができました。

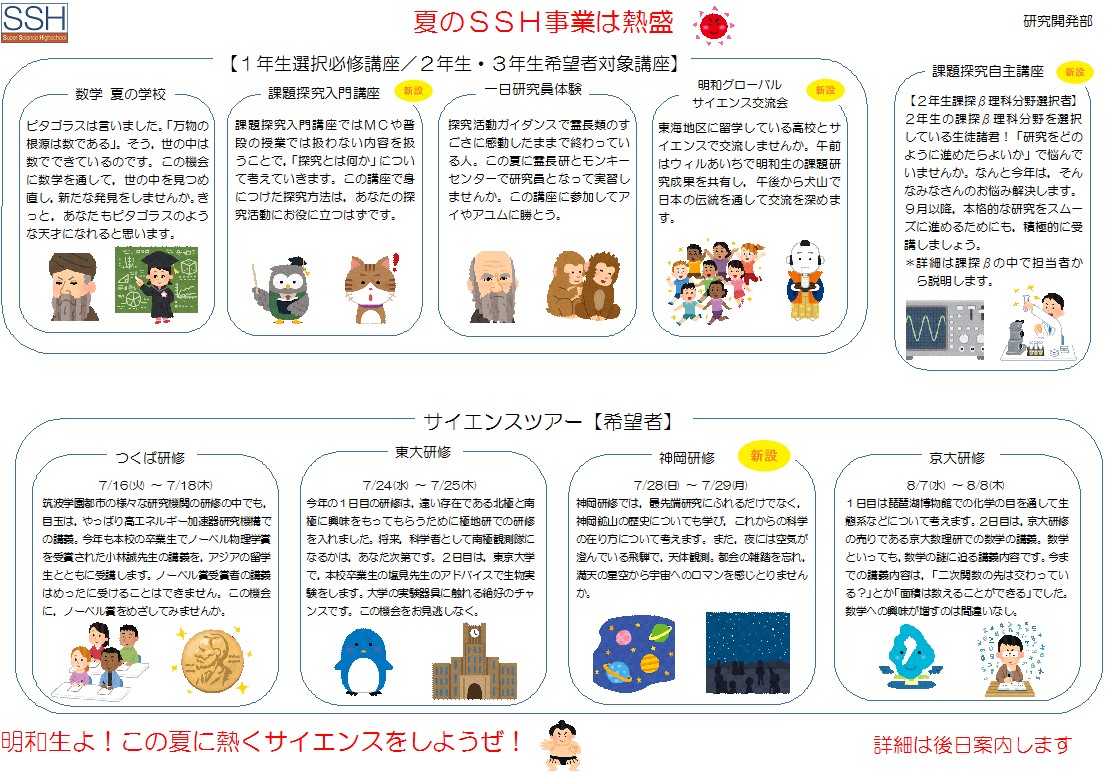
令和元年度ＳＳＨ「夏の事業」講座一覧

「数学　夏の学校」（講座番号1～9)の実施報告は、こちら

「一日研究員体験」（講座番号10)の実施報告は、こちら

「課題探究入門講座」（講座番号11～14)の実施報告は、こちら

「明和グローバル交流会」（講座番号20)の実施報告は、こちら

「課題探究自主講座」（講座番号30)の実施報告は、こちら

番号	講座名	講座種別	講師（敬称略）	期日・場所
1	集団での追跡と逃避	SSH特別講座「数学夏の学校」	名古屋大学大学院多元数理科学研究科教授　大平　徹	７月２３日(火) １３：３０～１５：３０本校（視聴覚教室）
1	追跡と逃避の問題は数学では18世紀からつづいている伝統のある問題です。また、昆虫、動物、鳥や人の群集の研究は最近様々な角度から研究が進んでいます。ここではこの２つの研究の流れを融合した集団追跡と逃避の問題について紹介を行います。
2	素数、ゼータ関数、多重ゼータ関数	SSH特別講座「数学夏の学校」	名古屋大学大学院多元数理科学研究科教授　松本　耕二	７月２６日（金）１３：３０～１５：３０本校（視聴覚教室）
2	素数の分布を研究することは、古来、人類を引きつけてやまないテーマですが、素数分布の研究で非常に重要な役割を果たすのがリーマンのゼータ関数です。今回の講座ではまずゼータ関数を定義し、素数とゼータ関数との結びつきを紹介します。そして、現在世界中で大変活発に研究が進められている、ゼータ関数を「多重化」した多重ゼータ関数と呼ばれる関数について解説したいと思います。
3	ブラックホールの数理	SSH特別講座「数学夏の学校」	名古屋大学大学院多元数理科学研究科教授　白水　徹也	８月１日（木）１３：３０～１５：３０本校（視聴覚教室）
3	ブラックホール時空の数学的構造の解説を平易な言葉で行います。そして、観測について一緒に考えてみたいと思います。
4	ゲーム理論	SSH特別講座「数学夏の学校」	名古屋大学大学院経済学研究科教授　花薗　誠	７月２５日（木）１３：３０～１５：３０本校（視聴覚教室）
4	ゲーム理論では、利害関係のある複数のプレーヤーがどのようにして各々の意思決定を行うかを研究します。勝敗の決まる対戦型ゲームの必勝法の分析にとどまらず、それぞれのプレーヤーの立場に立ってどのような意思決定が合理的かを考えます。経済学を始め、多くの社会科学における分析の基礎となっているゲーム理論を学び、合理的な意思決定の原理やその意味を探求しましょう。
5	トランプのシャッフルの話	SSH特別講座「数学夏の学校」	名古屋大学大学院多元数理科学研究科准教授　伊師　英之	８月９日（金）１０：００～１２：００本校（視聴覚教室）
5	トランプは、切れば切るほどよく混ざるのでしょうか？実際は、ある回数を境に、「あまり混ざっていない状態」から「よく混ざっている状態」に急激に変化することが、最先端の数学を用いて証明されています。その概略を説明します。
6	連分数とフォードの円	SSH特別講座「数学夏の学校」	名古屋大学大学院多元数理科学研究科准教授　糸　健太郎	８月５日（月）１０：００～１２：００本校（視聴覚教室）
6	連分数とはハシゴ状の形をした分数のことです。分数を連分数の形に表すことで、いままで見えてこなかった分数たちの間の幾何学的なつながりが見えてきます。このことを折り紙や円の作図などを交えながら楽しく学びましょう。自然界の至る所に現れる「黄金比」と連分数の関係も紹介します。
7	グラフ理論入門 Introduction to Graph Theory	SSH特別講座「数学夏の学校」	名古屋大学大学院多元数理科学研究科准教授　藤江　双葉	７月３１日(水) １３：３０～１５：３０本校（視聴覚教室）
7	電車の路線図では、駅と駅の「つながり方」が主に重要な情報で、実際の駅間の距離や配置などは省略して描かれます。このように「つながり方」に着目して抽象化された「点と、点と点を結ぶ辺」を考えるのがグラフ理論です。普段の授業で学ぶ数学とは少し雰囲気の異なるグラフの世界を、一緒に覗いてみましょう。 Have you heard of an area of Mathematics called Graph Theory、 a field that may be a little "different" from Mathematics in classroom? Color pens and a few pieces of paper are all you need!
8	対数と計算尺～西洋のそろばん～	SSH特別講座「数学夏の学校」	愛知県立明和高等学校教諭　服部　展之	８月８日(木) １０：００～１２：００本校（視聴覚教室）
8	電卓のない時代、九九や算盤がない欧米では、桁数の多い数の計算に苦労していました。ネイピアが対数を考案したおかげで、かけ算・割り算・平方根などの近似値計算が楽になり、自然科学の発展に多大な貢献をしました。対数の原理を学んだ上で、実際に計算尺を使った近似値計算を体験してもらいます。
9	江戸時代の数学	SSH特別講座「数学夏の学校」	名古屋大学(非常勤講師) 和算研究家　深川　英俊	７月２９日（月）１０：００～１２：００愛知県立瑞陵高等学校
9	日本ではそれぞれの荘園の中に計算担当者が居て、かれらは計算には強かったが数学者ではなかった。江戸時代の初めに中国数学が導入されるや江戸時代という国全体が平和な文化国家になるにつれ「数学」も次第に発展して独自の数学世界「和算」を作り上げた。現代では忘れ去られたこの数学世界は外国からも注目されている。電卓を持参。
10	京大霊長類研究所・日本モンキーセンター（ＪＭＣ）一日研究員体験	一日研究員体験	京大霊長類研究所（日本モンキーセンター所長）特別教授　松沢哲郎	７月１７日（水）１０：００～１６：００京大霊長類研究所およびＪＭＣ
10	午前中は京大霊長類研究所の松沢哲郎先生の研究室や実験施設で、午後は研究所に併設される日本モンキーセンター（JMC）を訪問し、研究員の一日を体験します。研究についてどんなイメージを持っていますか？自分で研究の一部を体験することで、多くのことを感じて、考える機会にしていきましょう。
11	探究活動「紙コップの不思議を探る」	課題探究入門講座	愛知県立明和高等学校教諭　小野　泉	８月６日（火１３：００～１６：３０本校（物理実験室）
11	紙コップに関する身近で不思議な現象について、探究的に解明する講座です。その日集まった初めてのメンバーでチームをつくり、ある現象について、複数の仮説を立て、それぞれの仮説について検証する方法を検討し、実際に実験して仮説の成否を判定し、あらたな仮説をたててさらに検証する、という探究活動の一連の流れを実践します。さらに、解明した不思議について、仮説の検証の過程を含めて、チームごとに発表します。さて、君は紙コップの不思議を解き明かせるか！？
12	探究活動生物の形態観察『透明骨格標本をつくろう！』	課題探究入門講座	愛知県立明和高等学校教諭　鈴木優美	８月２３日（金）９：３０～１１：００本校（生物実験室）
12	透明骨格標本とは、体を透明化して骨を染色し骨格を観察するための標本のことです。生物体全体を、ほぼそのままの状態で標本にするため、骨格の立体的な構造を詳しく観察することができます。生物体の構造や、透明化のメカニズムを学びながら標本を作製していきましょう。標本完成までには１ヶ月程度かかりますが、成功すれば大変美しい標本ができあがります。　※ 標本完成までに、１週間に２～３回　20分程度の作業（溶液の交換）を続ける必要があります。作業は昼休みを予定しています。講座の受講は標本完成まで継続して作業を行える生徒に限ります。
13	地理的な視点を通して「課題探究」の基礎を学ぶ	課題探究入門講座	愛知県立明和高等学校教諭　吉原　正記	８月９日（金）９：３０～１１：３０本校（２０８教室）
13	「課題探究」では、答えがない課題に対して仮説をたてて、自らの力で結論を導いていきます。しかし、実際に一人の力で研究を進めていくのはとても大変たいへんなことなので、「課題探究」ではチームで研究に取り組みます。しかし、チームが一つになって目標を達成することも、容易なことではありません。そこで、地理的な題材を利用して、チームが一つになることの大切さを学び、「課題研究」のチーム作りの基礎を学びます。なお、時間があれば、課題研究につながるような「戦略思考トレーニング」や統計の扱いなどについても簡単にふれたいと思います。
14	心理学研究法入門	課題探究入門講座	愛知県立明和高等学校教頭　松原正明	７月１８日（木）９：３０～１１：３０本校（２０８教室）
14	自身の「課題探究」に役立てることを目標として、心理学における様々な研究方法を概観する。特に、昨今注目されている「質的研究」について、その意義と方法を学びます。〈主なキーワード〉　・観察法　　・実験法　　・質問紙法　　・面接法　　・質的研究・研究倫理　　・グラウンデッドセオリーアプローチ（ＧＴＡ）
20	明和グローバルサイエンス交流会	国際交流講座	愛知県立明和高等学校	７月１９日（金）８：５０～１７：１０
20	日本にいながらにして科学を通して、東海地区に留学している外国人高校生・大学生約40名と交流します。午前は「ウィルあいち」で明和生が行った課題研究の英語による発表（ポスター及び口頭）を通して交流することにより、英語によるコミュニケーション能力の必要性を認識します。また、昼食（持参）をともにすることでお互いの文化について理解を深めます。午後からは、研修の場を犬山城下町に移します。犬山では、本校の生徒と外国人留学生で班を編制し、班別に【ものづくり研修】としてアート・テクノロジー・伝統が組み合わさった「からくり人形」の実演と見学、【文化的研修】として犬山城下町の散策などにより、午前で芽生えた国際感覚をさらに高めます。
30	理科課題研究基礎	課題研究自主講座（理科分野）	愛知県立明和高等学校理科教諭　全員	「課題探究β」担当教諭の指導可能日
30	この講座の目的は、「夏季休業中に課題研究に関する準備を進め、研究内容の質的向上をはかること」です。事前に「課題探究β」担当者の指導可能日を確認し、課題研究に取り組むグループで部活動やクラス活動の都合を話し合い、活動日、活動内容を決め、担当者に連絡します。実験、実習をともなう課題研究は、例年、研究進度が遅れがちで、発表会までに研究内容をしっかりまとめられないケースがよくあります。そこで、時間に余裕がある夏季休業中に、基礎実験や予備実験、先取り学習などを行えば、9月以降の研究が進められるし、研究内容を深めていくことができます。自主講座です。奮って参加してください！！　活動場所は、原則「課題探究β」の場所ですが、研究内容によって、郊外に出かけることもできます（大学の研究室、博物館など、フィールドワークも可）。担当者に相談してください。